Задание исследования
Провести исследование внутренней сходимости численного интегрирования методом Симпсона и трапеций различных функций, задаваемых с помощью языка С.
Подробное описание задачи и способы ее решения
Необходимо провести исследования так называемой внутренней сходимости численного интегрирования методами Симпсона и трапеций различных функций, задаваемых с помощью функций языка С. Предполагается, что отрезок интегрирования [a, b] разбит на n равных частей системой точек (сеткой).
![отрезок интегрирования [a, b] разбит на n равных частей системой точек отрезок интегрирования [a, b] разбит на n равных частей системой точек](https://studentreferat.ru/wp-content/uploads/2022/04/1-36.png)
Контроль внутренней сходимости заключается в циклическом вычислении приближенных значений интеграла для удваиваемого по сравнению со значением на предыдущем прохождении цикла числа n. Отношения абсолютной величины разности этих значений к абсолютной величине предыдущего приближенного значения принимается в качестве критерия достижения точности интеграла.
Построить зависимости количеств итераций от различных величин критерия точности.
Построить обратные зависимости критерия точности от количества итераций.
Повторить все вышеуказанные исследования для случая, когда при вычислении критерия точности разность значений интеграла относится не к предыдущему значению, а к точному значению аналитически вычисленного интеграла.
Исследовать влияние увеличения верхнего предела интегрирования на точность (при прочих неизменных условиях).
Метод трапеций
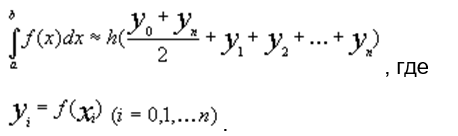
Метод Симпсона
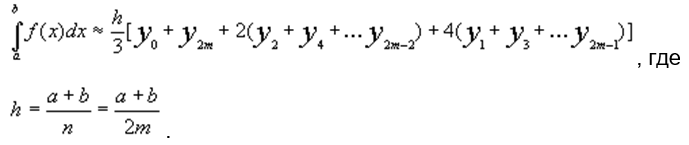
Результаты исследований
Таблица и график зависимости количества итераций от различных значений критерия точности:
Таблица 1
| Критерий точности | Количество итераций |
| -0,1676631 | 14 |
| -0,1518916 | 16 |
| -0,0046931 | 12 |
| -0,0026531 | 11 |
| -0,0002639 | 10 |
| -0,0001709 | 2 |
| -0,0001297 | 9 |
| -0,0000557 | 3 |
| -0,000025 | 8 |
| -0,0000198 | 4 |
| -0,0000096 | 5 |
| -0,0000038 | 6 |
| 0 | 15 |
| 0,0000052 | 7 |
| 0,071089 | 13 |
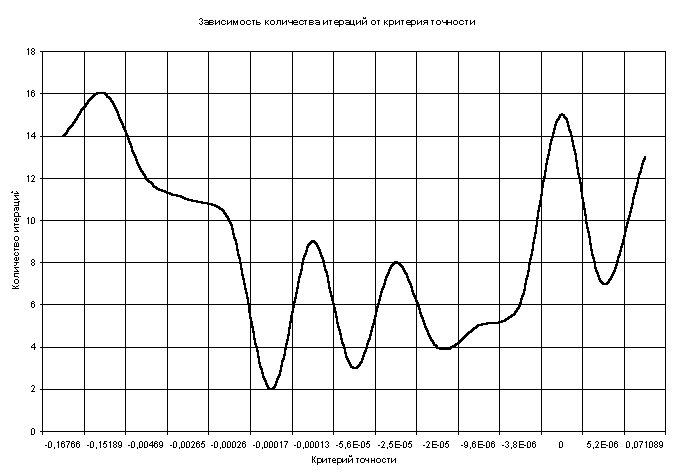
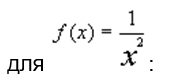
Таблица 2
| Критерий точности | Количество итераций |
| -0,1127271 | 16 |
| -0,0750288 | 15 |
| -0,0540677 | 14 |
| -0,0021415 | 12 |
| -0,0005711 | 11 |
| -0,0000458 | 9 |
| -0,0000381 | 2 |
| -0,0000191 | 3 |
| -0,000008 | 4 |
| -0,000004 | 5 |
| -0,0000019 | 7 |
| -0,0000002 | 6 |
| 0,000005 | 8 |
| 0,0002983 | 10 |
| 0,0164377 | 13 |
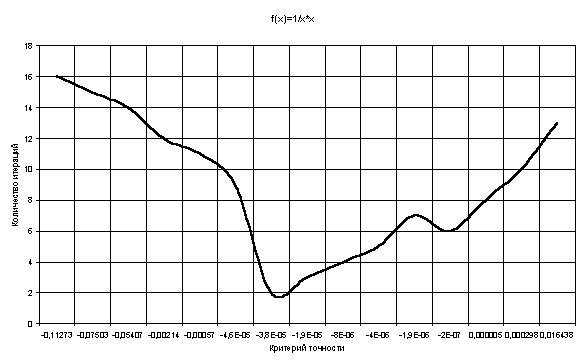
Таблица 3
| Критерий точности | Количество итераций |
| -0,0066709 | 13 |
| -0,0042367 | 14 |
| -0,0003561 | 10 |
| -0,0000016 | 5 |
| -0,000001 | 4 |
| 0,0000005 | 3 |
| 0,0000006 | 6 |
| 0,0000009 | 2 |
| 0,0000009 | 7 |
| 0,0000223 | 8 |
| 0,000056 | 9 |
| 0,0002782 | 11 |
| 0,0003474 | 12 |
| 0,005293 | 16 |
| 0,0053267 | 15 |
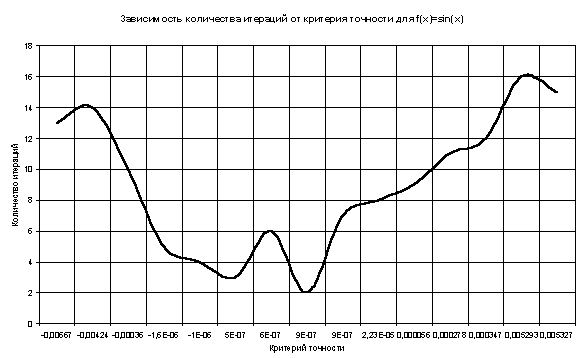
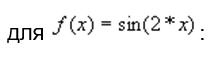
Таблица 4
| Критерий точности | Критерий точности |
| -61,4469795 | 12 |
| -5,714047 | 3 |
| -1,0215755 | 13 |
| -0,7241433 | 2 |
| -0,5121117 | 4 |
| -0,3222643 | 11 |
| -0,2163614 | 7 |
| -0,1536629 | 9 |
| -0,0930261 | 14 |
| 0,0353183 | 16 |
| 0,057059 | 15 |
| 0,1697371 | 5 |
| 0,2025534 | 10 |
| 0,2504728 | 6 |
| 0,6202592 | 8 |
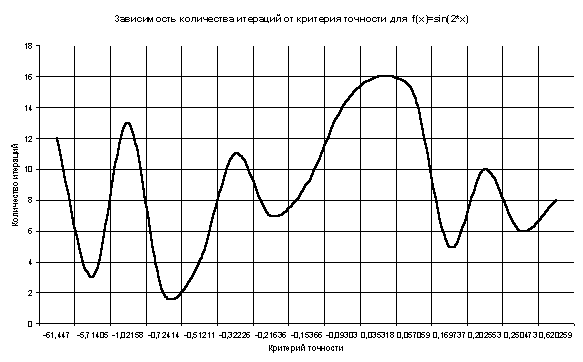
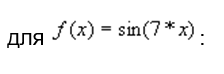
таблица 5
| Критерий точности | Количество итераций |
| -0,0119308 | 16 |
| -0,0007834 | 13 |
| -0,0000079 | 3 |
| -0,0000041 | 4 |
| -0,0000037 | 7 |
| -0,0000027 | 5 |
| -0,0000027 | 6 |
| -0,000002 | 8 |
| -0,0000016 | 2 |
| 0,0000003 | 10 |
| 0,0000062 | 9 |
| 0,0000385 | 11 |
| 0,0000802 | 12 |
| 0,0005452 | 15 |
| 0,0016689 | 14 |
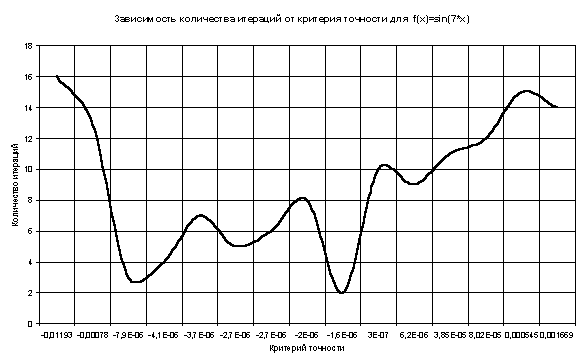
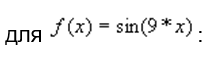
Таблица 6
| Критерий точности | Количество итераций |
| -0,0026286 | 16 |
| -0,0012416 | 14 |
| -0,0000118 | 3 |
| -0,0000107 | 4 |
| -0,0000046 | 5 |
| -0,0000046 | 9 |
| -0,0000028 | 6 |
| -0,0000021 | 7 |
| -0,0000005 | 2 |
| 0,0000011 | 10 |
| 0,0000018 | 8 |
| 0,0000023 | 11 |
| 0,000058 | 12 |
| 0,0001049 | 13 |
| 0,0027928 | 15 |
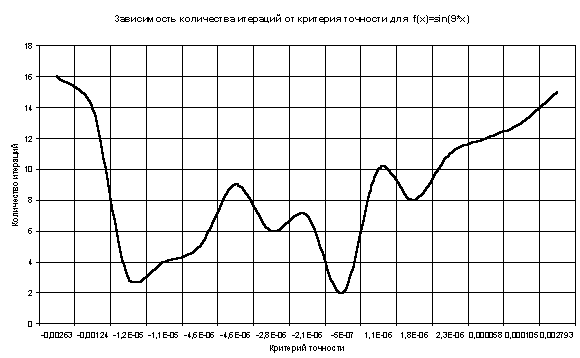
Таблицы и графики зависимости значений критерия точности от количества итераций.
Таблица 7
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||
| Критерий точности | Количество итераций | Критерий точности | Количество итераций |
| -0,0001709 | 2 | -0,0001932 | 2 |
| -0,0000557 | 3 | -0,0000629 | 3 |
| -0,0000198 | 4 | -0,0000224 | 4 |
| -0,0000096 | 5 | -0,0000108 | 5 |
| -0,0000038 | 6 | -0,0000043 | 6 |
| 0,0000052 | 7 | 0,0000058 | 7 |
| -0,000025 | 8 | -0,0000283 | 8 |
| -0,0001297 | 9 | -0,0001466 | 9 |
| -0,0002639 | 10 | -0,0002983 | 10 |
| -0,0026531 | 11 | -0,002998 | 11 |
| -0,0046931 | 12 | -0,0052891 | 12 |
| 0,071089 | 13 | 0,0797403 | 13 |
| -0,1676631 | 14 | -0,2014365 | 14 |
| 0 | 15 | 0 | 15 |
| -0,1518916 | 16 | -0,1518916 | 16 |
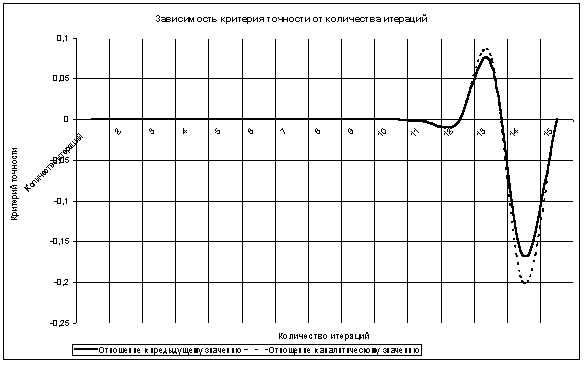
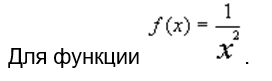
Таблица 8
| По отношению к предыдущему значению | По отношению к аналитическому значению | |||||
| Критерий точности | Количество итераций | Критерий точности | Количество итераций | |||
| -0,0000381 | 2 | -0,0000666 | 2 | |||
| -0,0000191 | 3 | -0,0000335 | 3 | |||
| -0,000008 | 4 | -0,0000141 | 4 | |||
| -0,000004 | 5 | -0,0000069 | 5 | |||
| -0,0000002 | 6 | -0,0000004 | 6 | |||
| -0,0000019 | 7 | -0,0000033 | 7 | |||
| 0,000005 | 8 | 0,0000088 | 8 | |||
| -0,0000458 | 9 | -0,0000802 | 9 | |||
| 0,0002983 | 10 | 0,000522 | 10 | |||
| -0,0005711 | 11 | -0,0009997 | 11 | |||
| -0,0021415 | 12 | -0,0037465 | 12 | |||
| 0,0164377 | 13 | 0,0286955 | 13 | |||
| -0,0540677 | 14 | -0,0959378 | 14 | |||
| -0,0750288 | 15 | -0,1259331 | 15 | |||
| -0,1127271 | 16 | -0,1750124 | 16 | |||
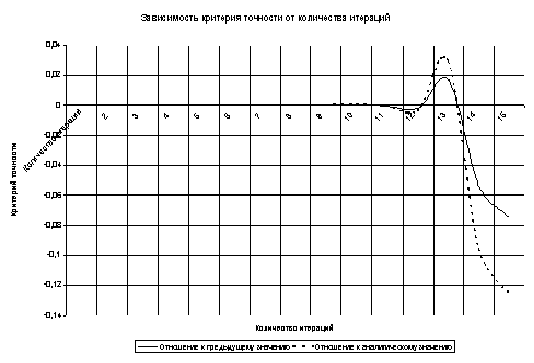
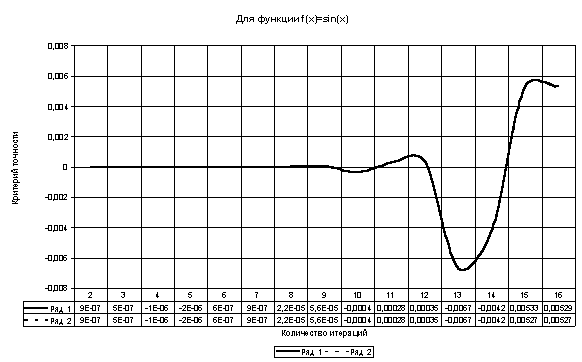
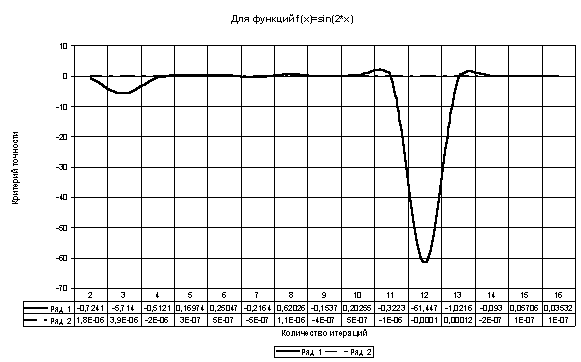
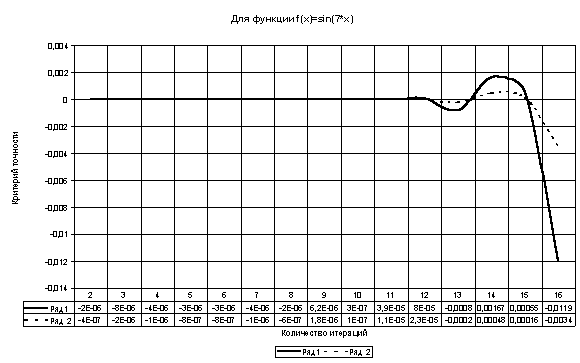
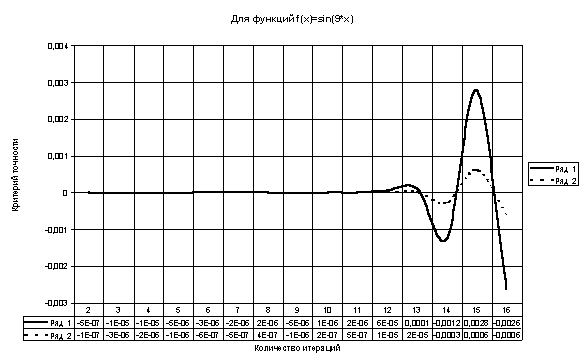
Таблица 9
Сравнительные результаты
| Метод трапеции n = 1000000 | Метод Симпсона
n = 1000000 |
Аналитический результат | Функция | Пределы |
| 4,5051475 | 4,5240183 | 4,49980967 | f(x) = 1/x | 0,1 – 9 |
| 1,7491462 | 1,7500761 | 1,791756469 | f(x) = 1/x*x | 0,3 – 5 |
| 1,9991885 | 1,9999505 | 2 | f(x) = sin(x) | 0 – π |
| -0,0000512 | 0,000003 | 0 | f(x) = sin(2*x) | 0 – π |
| 0,2857157 | 0,2856935 | 0,285714285 | f(x) = sin(7*x) | 0 – π |
| 0,2222053 | 0,2222133 | 0,222222222 | f(x) = sin(9*x) | 0 – π |
Таблица 10
Влияние увеличения верхнего предела на точность интегрирования
| Аналитическое значение | Практическое значение | Верхний предел | Погрешность |
| 4,49980967 | 4,5217996 | 9 | -0,02198993 |
| 4,605170186 | 4,624969 | 10 | -0,019798814 |
| 4,787491743 | 4,8039412 | 12 | -0,016449457 |
| 4,941642423 | 4,9557843 | 14 | -0,014141877 |
| 5,075173815 | 5,0875444 | 16 | -0,012370585 |
| 5,192956851 | 5,2039275 | 18 | -0,010970649 |
| 5,298317367 | 5,3082042 | 20 | -0,009886833 |
Следовательно, увеличение верхнего предела приводит к увеличению точности интегрирования.
Текст программы
/* Курсовая работа по информатике
«Исследование точности численного интегрирования»
«Research of Accuracy of Numerical Integration»
Преподаватель:
Студенты: Степанов А. Г.
Черепанов К. А
Группа: Р-207
*/
# include <stdio.h>
# include <io.h>
# include <stdlib.h>
# include <iostream.h>
# include <string.h>
# include <math.h>
int main ()
{
FILE *fp; /*указатель на поток*/
int n,i,t,j,N;
float a,b,h,Sum[100],x,y,coa;
printf(«Research of Accuracy of Numerical Integrationn»);
/*Ввод точности вычисления*/
printf(«Enter accuracy of calculation n= «);
scanf(«%d»,&n);
/*Ввод начала интегрирования*/
printf(«Enter beginnings of integration= «);
scanf(«%f»,&a);
/*Ввод предела интегрирования*/
printf(«Enter limit of integration= «);
scanf(«%f»,&b);
/*Открытие файла-источника*/
while((fp=fopen(«data3.xls»,»w»))==NULL)
{
puts(«Error!!! Can’t open file nInput name of filen»);
}
/*Ввод количества итераций*/
printf(«Enter number of Itteration N= «);
scanf(«%d»,&N);
/*Вычисление шага интегрирования*/
h=(a+b)/n;
printf(«Step=%.3fn»,h);
/*******Вычисление интеграла методом трапеций*******/
for(j=1;j<=N;j++)
{
h=(a+b)/(int(pow(2,j-1))*n);
Sum[j]=0;
for(i=0;i<=(int(pow(2,j-1))*n);i++)
{
x=a+i*h;
if(i==0)
t=1;
else
t=2;
y=t*(h/2)*(sin(2*x));
Sum[j]=Sum[j]+y;
}
if (j>1)
{
coa=(Sum[j]-Sum[j-1])/Sum[j-1];
printf(«Criterion of accuracy=%.5f Number of iteration=%dn»,coa,j);
fprintf(fp,»%.7ft»,coa);
fprintf(fp,»%dtn»,j);
}
}
printf(«The sum by a method of trapezes=%.7fn»,Sum[1]);
fprintf(fp,»The sum by a method of trapezes=%.7fn»,Sum[1]);
/*******Вычисление интеграла методом Симпсона*******/
for(j=1;j<=N;j++)
{
h=(a+b)/(int(pow(2,j-1))*n);
Sum[j]=0;
for(i=0;i<=(int(pow(2,j-1))*n);i++)
{
x=a+i*h;
if(i==0||i==n)
t=1;
else
{
if(i%2==0)
t=2;
else
t=4;
}
y=t*(h/3)*(sin(2*x));
Sum[j]=Sum[j]+y;
}
if (j>1)
{
coa=(Sum[j]-Sum[j-1])/Sum[j-1];
printf(«Criterion of accuracy=%.5f Number of iteration=%dn»,coa,j);
fprintf(fp,»%.7ft»,coa);
fprintf(fp,»%dtn»,j);
}
}
printf(«The sum by a Simpson’s method= %.7fn»,Sum[1]);
fprintf(fp,»The sum by a Simpson’s method=%.7fn»,Sum[1]);
scanf(«%d»,&b);
}